tidyverseDay 3 Walkthrough
# Load the required packages
library(dplyr)
Attaching package: 'dplyr'The following objects are masked from 'package:stats':
filter, lagThe following objects are masked from 'package:base':
intersect, setdiff, setequal, unionlibrary(ggplot2)
library(moderndive)
library(infer)# For reproducibility
set.seed(2024)
# Create vectors of sport ball types and their proportions
types_of_sport_balls <- c("Basketball", "Pickleball", "Tennis Ball",
"Football/Soccer", "American Football")
proportion_of_each_type <- c(0.2, 0.15, 0.3, 0.25, 0.1)
# Create a tibble of 1200 sport balls that will act as our population
store_ball_inventory <- tibble(
ball_ID = 1:1200,
ball_type = sample(x = types_of_sport_balls,
size = 1200,
replace = TRUE,
prob = proportion_of_each_type
)
)# Use glimpse to explore the structure of the dataset
glimpse(store_ball_inventory)Rows: 1,200
Columns: 2
$ ball_ID <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 2…
$ ball_type <chr> "Pickleball", "Football/Soccer", "Basketball", "Basketball", "Football/Soccer", "Basketball", "Footb…# Create a count of ball_type
store_ball_inventory |>
count(ball_type)# A tibble: 5 × 2
ball_type n
<chr> <int>
1 American Football 117
2 Basketball 252
3 Football/Soccer 299
4 Pickleball 187
5 Tennis Ball 345# Determine the proportion of pickleballs in the inventory
p_df <- store_ball_inventory |>
summarize(prop_pickle = mean(ball_type == "Pickleball"))
# Convert p to a numeric value
p <- p_df$prop_pickle
# Or using the tidyverse
p <- p_df |> pull(prop_pickle)# Retrieve a sample of 50 balls from the inventory
ball_sample <- store_ball_inventory |>
slice_sample(n = 50, replace = FALSE)
# Determine the proportion of pickleballs in the sample
ball_sample |>
summarize(prop_pickle = mean(ball_type == "Pickleball"))# A tibble: 1 × 1
prop_pickle
<dbl>
1 0.14# Retrieve another sample of 50 balls from the inventory
ball_sample2 <- store_ball_inventory |>
slice_sample(n = 50, replace = FALSE)
# Determine the proportion of pickleballs in the sample
ball_sample2 |>
summarize(prop_pickle = mean(ball_type == "Pickleball"))# A tibble: 1 × 1
prop_pickle
<dbl>
1 0.1# Use `rep_slice_sample()` from the `infer` package
ball_samples <- store_ball_inventory |>
rep_slice_sample(n = 50, reps = 1000, replace = FALSE)# Determine sample proportions with `dplyr`
props_pickle <- ball_samples |>
summarize(prop_pickle = mean(ball_type == "Pickleball"))
# Create a histogram of the sample proportions
ggplot(props_pickle, aes(x = prop_pickle)) +
geom_histogram(bins = 15, color = "white") +
labs(x = "Sample proportion",
title = "Histogram of 1000 sample proportions of Pickleballs") 
# Using the simulations, calculate the standard deviation of the
# sample proportions
se_sample_props <- props_pickle |>
summarize(sd(prop_pickle)) |>
pull()
# Using the formula for the standard error of a sample proportion
n <- 50
se_sample_props_formula <- sqrt(p * (1 - p) / n)# Create a function to calculate the standard error of sample proportions
# using simulation
se_sample_props <- function(size, repetitions = 1000, type = "Pickleball") {
props <- store_ball_inventory |>
rep_slice_sample(n = size, reps = repetitions, replace = FALSE) |>
summarize(prop = mean(ball_type == type))
se_sample_props <- props |>
summarize(sd(prop)) |>
pull()
return(se_sample_props)
}
# Standard errors for different sample sizes
se_sample_props_20 <- se_sample_props(20)
se_sample_props_50 <- se_sample_props(50)
se_sample_props_100 <- se_sample_props(100)(1.1) What is the purpose of using the sample() function in the code provided?
A. To randomly select a subset of the population without replacement.
B. To calculate the mean value of a numeric variable.
C. To remove missing values from the dataset.
D. To calculate the population parameters.
(1.2) In the context of the sporting goods store example, what does the sample proportion of pickleballs represent?
A. The actual number of pickleballs in the entire inventory.
B. The proportion of pickleballs in a random sample taken from the inventory.
C. The total number of all types of sport balls in the inventory.
D. The probability of not selecting a pickleball from the population.
(1.3) What does the function rep_slice_sample() do in the sampling process?
A. It generates multiple samples from a population, each with the same size.
B. It creates a histogram of sample proportions.
C. It removes duplicate samples from the dataset.
D. It replicates the population to simulate different proportions.
(1.4) Why is the standard error calculated when taking samples from a population?
A. To ensure that the sample is randomly selected. B. To estimate the total number of items in the population.
C. To adjust the sample size for better accuracy.
D. To measure how much sample proportions vary from the population proportion.
(1.5) How does increasing the sample size affect the standard error of the sample proportions?
A. It increases the standard error because more data points create more variation.
B. It decreases the standard error, leading to more precise estimates of the population proportion.
C. It has no effect on the standard error.
D. It changes the population proportion directly.
(7.1) What is the purpose of using the sample() function in the code provided?
Correct Answer:
A. To randomly select a subset of the population without replacement.
Explanation:
The sample() function is used to randomly select a subset of observations from the population, which helps create samples for analysis.
(7.2) In the context of the sporting goods store example, what does the sample proportion of pickleballs represent?
Correct Answer:
B. The proportion of pickleballs in a random sample taken from the inventory.
Explanation:
The sample proportion reflects how many pickleballs appear in a random sample of the inventory, not the entire population.
(7.3) What does the function rep_slice_sample() do in the sampling process?
Correct Answer:
A. It generates multiple samples from a population, each with the same size.
Explanation:
The rep_slice_sample() function takes repeated samples of the same size from a population, allowing for the simulation of sampling variability.
(7.4) Why is the standard error calculated when taking samples from a population?
Correct Answer:
D. To measure how much sample proportions vary from the population proportion.
Explanation:
The standard error measures the variability in the sample proportions and indicates how close the sample proportions are to the true population proportion.
(7.5) How does increasing the sample size affect the standard error of the sample proportions?
Correct Answer:
B. It decreases the standard error, leading to more precise estimates of the population proportion.
Explanation:
Larger sample sizes reduce the variability in sample proportions, which decreases the standard error and improves the precision of the estimate of the population proportion.
# Create a tibble of 9500 adults and their corresponding commute times
# in minutes
# This acts as a population of adults and their commute times
commute_data <- tibble(
person_ID = 1:9500,
commute_time = rnorm(n = 9500, mean = 30, sd = 10)
)# Choose sample size
sample_size <- 100
# Generate a sample
set.seed(2024)
commute_sample <- commute_data |>
slice_sample(n = sample_size, replace = FALSE)
# Calculate the sample mean
sample_mean <- commute_sample |>
summarize(mean(commute_time)) |>
pull()
sample_mean[1] 29.16929# Calculate the standard deviation
sample_sd <- commute_sample |>
summarize(sd(commute_time)) |>
pull()
sample_sd[1] 10.06214# Calculate the population mean
population_mean <- commute_data |>
summarize(mean(commute_time)) |>
pull()
mu <- population_mean
mu[1] 29.98266# Calculate the population standard deviation
population_sd <- commute_data |>
summarize(sd(commute_time)) |>
pull()
sigma <- population_sd
sigma[1] 10.02985# Calculate the margin of error
z_star <- qnorm(p = 0.975) # Assumes a normal distribution
margin_of_error <- z_star * (sigma / sqrt(sample_size))
# Recall the point estimate
point_estimate <- sample_mean
# Calculate the confidence interval
lower_bound <- point_estimate - margin_of_error
upper_bound <- point_estimate + margin_of_error
# Display the confidence interval
c(lower_bound, upper_bound)[1] 27.20347 31.13510# Remember the population parameter (we usually don't know it)
between(mu, lower_bound, upper_bound) # dplyr::between()[1] TRUE# Calculate the margin of error
t_star <- qt(p = 0.975, df = sample_size - 1) # t-distribution
margin_of_error_t <- t_star * (sample_sd / sqrt(sample_size))
# Same point estimate
point_estimate_t <- sample_mean
# Calculate the confidence interval
lower_bound_t <- point_estimate_t - margin_of_error_t
upper_bound_t <- point_estimate_t + margin_of_error_t
# Display the confidence interval
c(lower_bound_t, upper_bound_t)[1] 27.17274 31.16584# Remember the population parameter (we usually don't know it)
between(mu, lower_bound_t, upper_bound_t)[1] TRUEWe are “95% confident” that the true mean commute time for this population of adults is between 27.1727413 and 31.1658354 minutes. This is the same as saying that if we were to take many samples of size 100 and calculate the confidence interval for each sample, we would expect 95% of those intervals to contain the true population mean of 29.9826594.
(8.1) What does the sample mean represent in general?
A. The mean for the entire population.
B. The mean for the smaller collection from the larger group of interest.
C. The mean for those outside the sample.
D. The population parameter.
(8.2) Which of the following describes the purpose of calculating a margin of error?
A. To estimate the standard deviation of the sample.
B. To account for the variability in sample means and create a confidence interval.
C. To find the population mean directly.
D. To calculate the proportion of people with a commute time under the sample mean.
(8.3) How is the margin of error calculated when the population standard deviation is known?
A. Using a t-distribution and the sample standard deviation.
B. Using a z-distribution and the sample standard deviation.
C. Using a z-distribution and the population standard deviation.
D. Using a t-distribution and the population standard deviation.
(8.4) When using the \(t\)-distribution for confidence intervals, why is it used instead of the \(z\)-distribution?
A. The t-distribution adjusts for larger sample sizes.
B. The t-distribution is used when the sample standard deviation is smaller than the population standard deviation. C. The t-distribution accounts for the population mean being known.
D. The t-distribution is used when the population standard deviation is unknown.
(8.5) What does it mean to be “95% confident” in the confidence interval calculated?
A. That 95% of similarly constructed confidence intervals from repeated samples would contain the true population mean. B. That the population mean is exactly equal to the sample mean.
C. That 95% of the data points in the sample fall within the interval.
D. That 95% of the sample means from different samples will be the same as the sample mean in this confidence interval.
(8.1) What does the sample mean represent in this context of commute times?
Correct Answer:
B. The mean for the smaller collection from the larger group of interest.
Explanation:
The sample mean is the average for those in the sample.
(8.2) Which of the following describes the purpose of calculating a margin of error?
Correct Answer:
B. To account for the variability in sample means and create a confidence interval.
Explanation:
The margin of error helps account for the natural variation in different samples and is used to create a range (confidence interval) around the sample mean where the true population mean likely falls.
(8.3) How is the margin of error calculated when the population standard deviation is known?
Correct Answer:
C. Using a z-distribution and the population standard deviation.
Explanation:
When the population standard deviation is known, the margin of error is calculated using the z-distribution, reflecting normal distribution assumptions.
(8.4) When using the t-distribution for confidence intervals, why is it used instead of the z-distribution?
Correct Answer:
D. The t-distribution is used when the population standard deviation is unknown.
Explanation:
The t-distribution is used when we do not know the population standard deviation, and it adjusts for the added uncertainty in estimating this value using the sample standard deviation.
(8.5) What does it mean to be “95% confident” in the confidence interval calculated?
Correct Answer:
A. That 95% of similarly constructed confidence intervals from repeated samples would contain the true population mean.
Explanation:
Being 95% confident means that if we repeatedly took samples and calculated confidence intervals, 95% of those intervals would capture the true population mean.
# Assume we only have a sample of 100 adults and their commute times
commute_sample# A tibble: 100 × 2
person_ID commute_time
<int> <dbl>
1 5698 63.2
2 4645 20.0
3 3488 18.6
4 8297 31.1
5 7802 41.8
6 1035 24.4
7 6045 32.7
8 7230 19.3
9 7420 12.0
10 8590 27.5
# ℹ 90 more rowsinfer Framework
# Bootstrapping the sample
set.seed(2024)
one_bootstrap <- commute_sample |>
specify(response = commute_time) |>
generate(reps = 1, type = "bootstrap")
one_bootstrapResponse: commute_time (numeric)
# A tibble: 100 × 2
# Groups: replicate [1]
replicate commute_time
<int> <dbl>
1 1 34.1
2 1 40.7
3 1 31.5
4 1 27.3
5 1 42.2
6 1 42.3
7 1 25.6
8 1 51.4
9 1 19.7
10 1 43.9
# ℹ 90 more rows# Calculate the mean of the bootstrap sample
one_bootstrap |>
calculate(stat = "mean") |>
pull()[1] 29.51807# Bootstrapping 1000 samples
many_bootstraps <- commute_sample |>
specify(response = commute_time) |>
generate(reps = 1000, type = "bootstrap")
many_bootstrapsResponse: commute_time (numeric)
# A tibble: 100,000 × 2
# Groups: replicate [1,000]
replicate commute_time
<int> <dbl>
1 1 27.7
2 1 27.9
3 1 20.3
4 1 22.9
5 1 31.2
6 1 25.8
7 1 33.9
8 1 19.3
9 1 27.8
10 1 25.8
# ℹ 99,990 more rows# Calculate the mean of each bootstrap sample
bootstrap_means <- many_bootstraps |>
calculate(stat = "mean")
bootstrap_meansResponse: commute_time (numeric)
# A tibble: 1,000 × 2
replicate stat
<int> <dbl>
1 1 30.1
2 2 28.9
3 3 30.0
4 4 30.2
5 5 28.4
6 6 28.8
7 7 29.8
8 8 30.2
9 9 28.9
10 10 29.6
# ℹ 990 more rows# Create a histogram of the bootstrap means
ggplot(bootstrap_means, aes(x = stat)) +
geom_histogram(bins = 30, color = "white") +
labs(x = "Bootstrap sample mean",
title = "Histogram of 1000 bootstrap sample means")
# Calculate the bootstrap confidence interval in two ways since bell-shaped
bootstrap_percentile_ci <- bootstrap_means |>
get_confidence_interval(level = 0.95, type = "percentile")
bootstrap_se_ci <- bootstrap_means |>
get_confidence_interval(level = 0.95,
type = "se",
point_estimate = sample_mean)We are “95% confident” that the true mean commute time for this population of adults is between 27.3707695 and 31.1042937 minutes. This is the same as saying that if we were to take many samples of size 100 and calculate the confidence interval for each sample, we would expect 95% of those intervals to contain the true population mean of 29.9826594.
# Show the histogram of bootstrap means with the confidence interval
# and the population parameter (not usually known)
bootstrap_means |>
visualize() +
shade_confidence_interval(endpoints = bootstrap_percentile_ci) +
geom_vline(xintercept = mu, color = "purple", linewidth = 2)
(9.1) What is the purpose of bootstrapping?
A. To calculate the exact population mean from a sample.
B. To generate multiple samples from the population without replacement.
C. To estimate the sampling distribution of the sample mean by resampling the original sample.
D. To directly calculate the confidence interval without using the sample data.
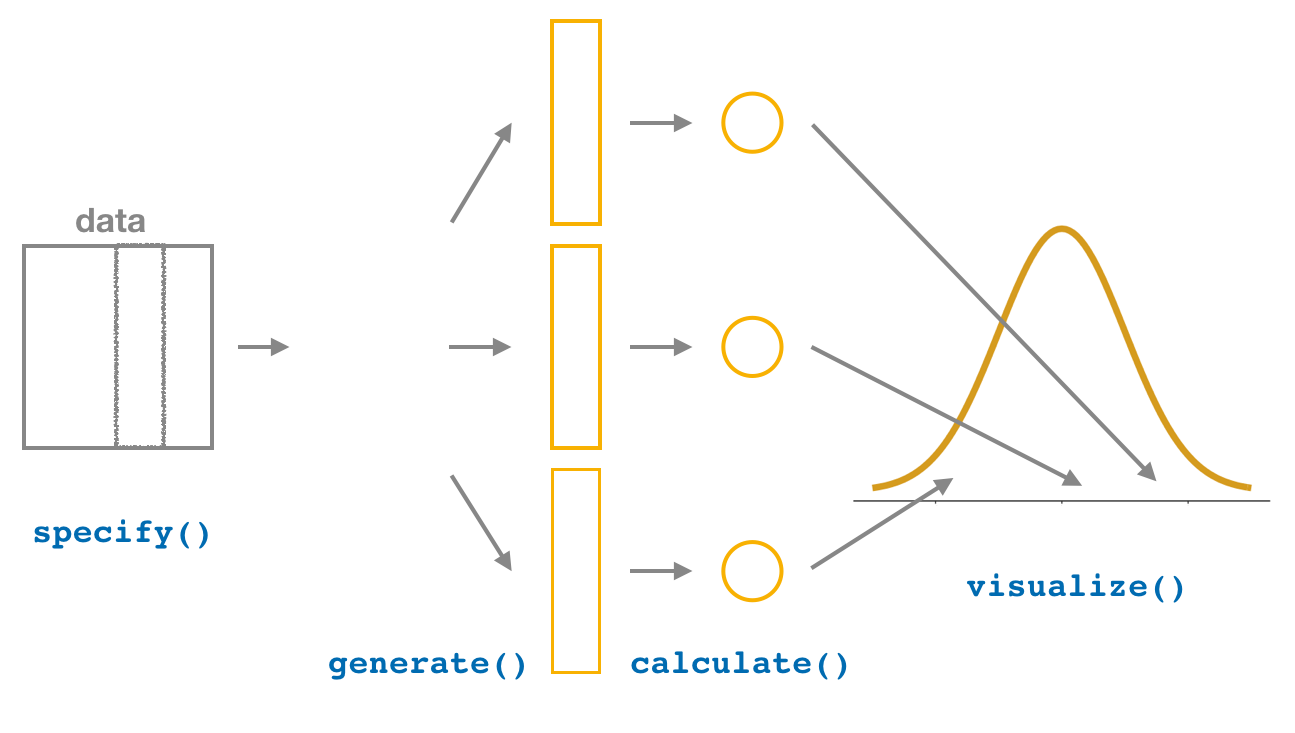
(9.2) In the bootstrapping process, what does the generate(reps = 1000, type = "bootstrap") function do?
A. It creates 1000 random samples from the original population.
B. It creates 1000 random samples with replacement from the original sample.
C. It creates 1000 exact copies of the population.
D. It creates 1000 different statistics from the original population.
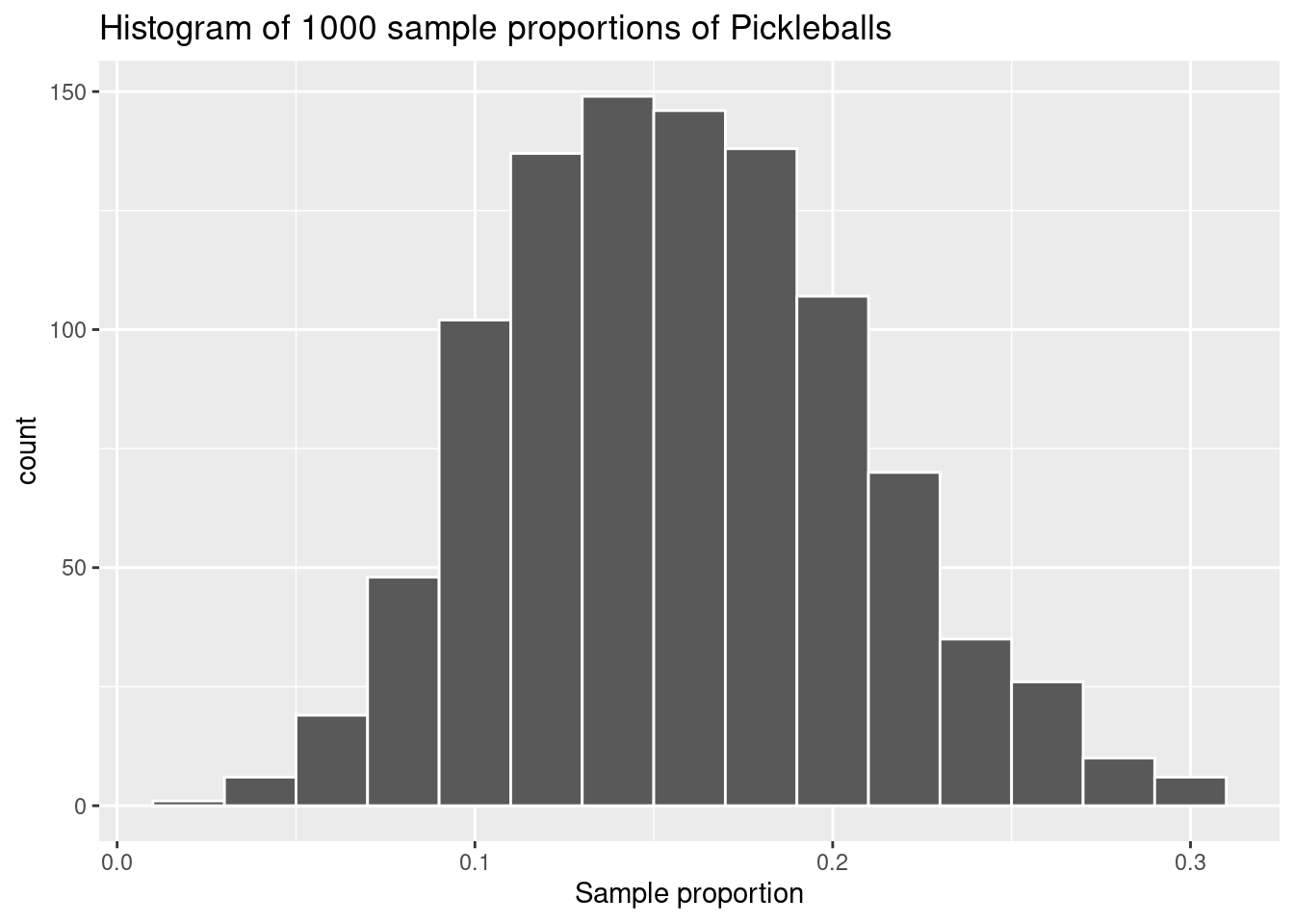
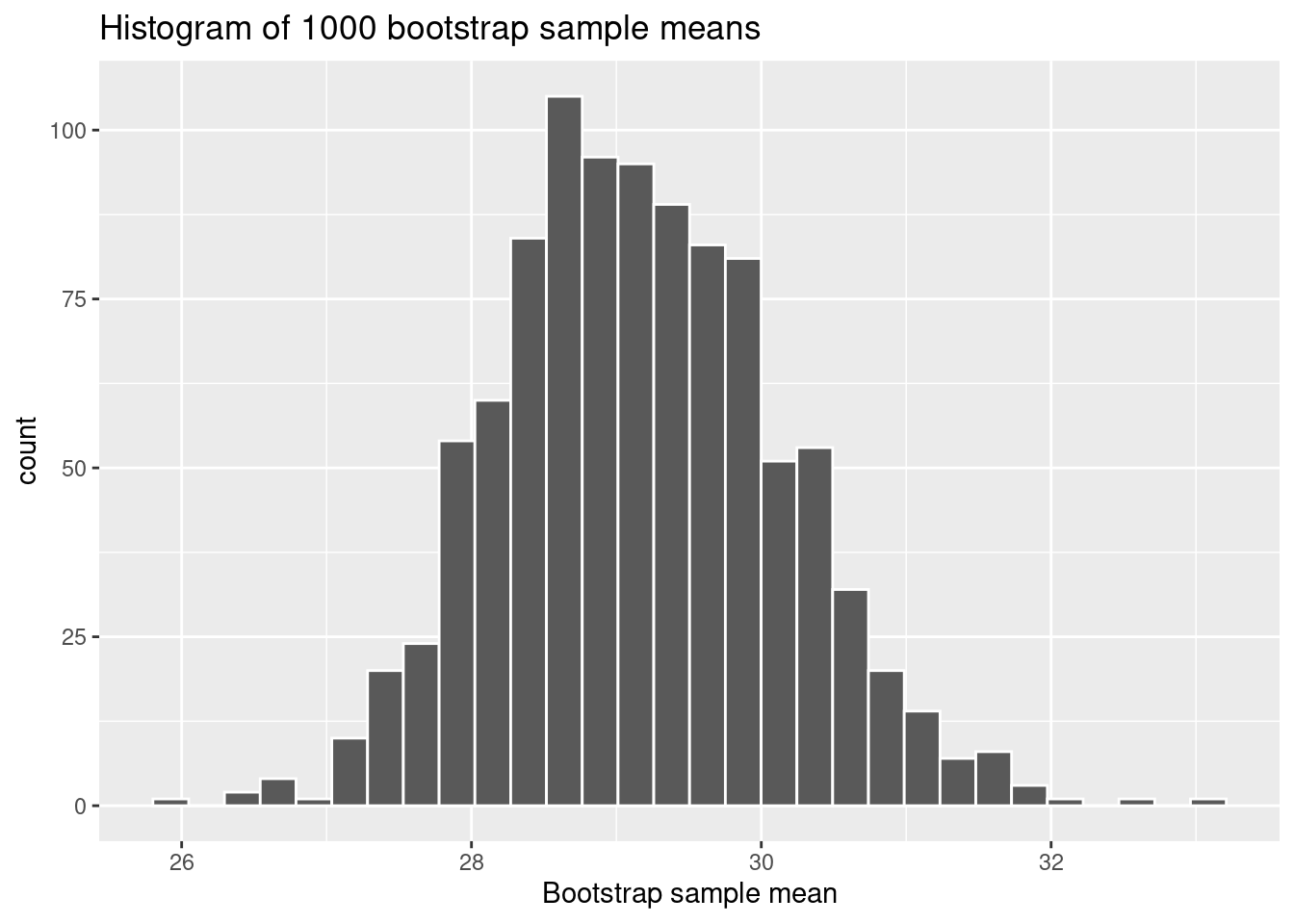
(9.3) What does the histogram of bootstrap sample means represent?
A. The distribution of sample means from the 1000 bootstrap samples.
B. The distribution of values in the original population.
C. The distribution of the population means calculated from the original sample.
D. The actual population mean with 95% certainty.
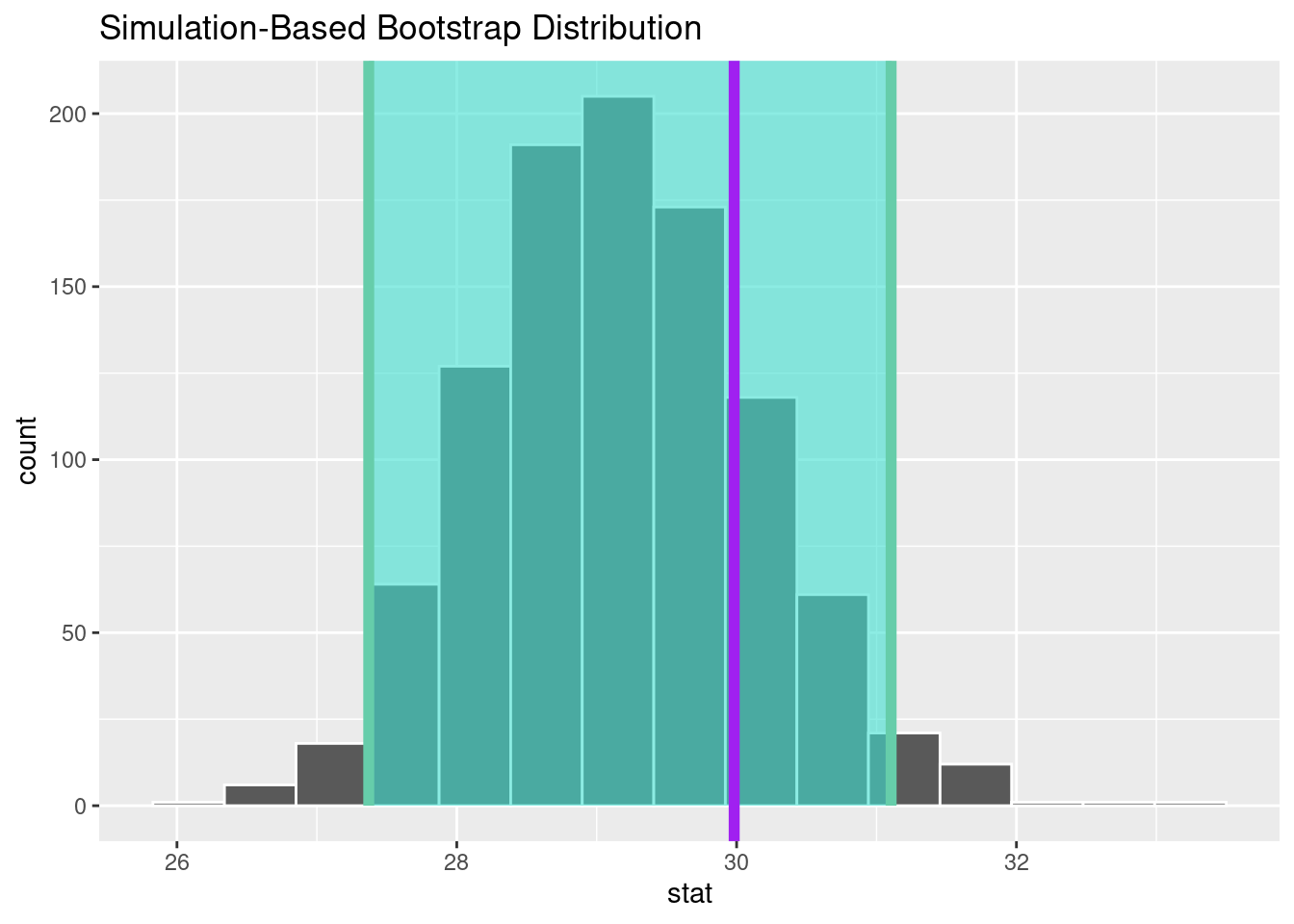
(9.4) How is the bootstrap percentile confidence interval calculated?
A. By calculating the standard deviation of the bootstrap samples.
B. By using the \(t\)-distribution to calculate the margin of error.
C. By taking the 2.5th and 97.5th percentiles of the bootstrap sample means.
D. By calculating the \(z\)-distribution based on the sample size.
(9.5) What does it mean to be “95% confident” in the bootstrap confidence interval?
A. That 95% of the bootstrap samples contain the population mean.
B. That the true population mean lies within the interval for 95% of all bootstrap samples.
C. That 95% of the population values fall within the confidence interval. D. That if we repeated the bootstrapping process many times, 95% of the confidence intervals would contain the true population mean.
(9.1) What is the purpose of bootstrapping in the context of this commute time example?
Correct Answer:
C. To estimate the sampling distribution of the sample mean by resampling the original sample.
Explanation:
Bootstrapping allows us to approximate the sampling distribution by repeatedly resampling the original sample with replacement and calculating the statistic of interest (in this case, the mean).
(9.2) In the bootstrapping process, what does the generate(reps = 1000, type = "bootstrap") function do?
Correct Answer:
A. It generates 1000 random samples with replacement from the original sample.
Explanation:
The generate() function resamples the original data with replacement to create 1000 new bootstrap samples, which are used to estimate the sampling distribution of the sample mean.
(9.3) What does the histogram of bootstrap sample means represent?
Correct Answer:
B. The distribution of sample means from the 1000 bootstrap samples.
Explanation:
The histogram shows the variability in sample means across the 1000 bootstrap samples, giving insight into the sampling distribution of the sample mean.
(9.4) How is the bootstrap percentile confidence interval calculated?
Correct Answer:
C. By taking the 2.5th and 97.5th percentiles of the bootstrap sample means.
Explanation:
The bootstrap percentile confidence interval is found by identifying the lower and upper bounds at the 2.5th and 97.5th percentiles of the bootstrap sample means.
(9.5) What does it mean to be “95% confident” in the bootstrap confidence interval?
Correct Answer:
D. That if we repeated the bootstrapping process many times, 95% of the confidence intervals would contain the true population mean.
Explanation:
Being “95% confident” means that if we repeatedly generated bootstrap samples and calculated confidence intervals, 95% of those intervals would capture the true population mean.