tidyverseDay 3 Exercises
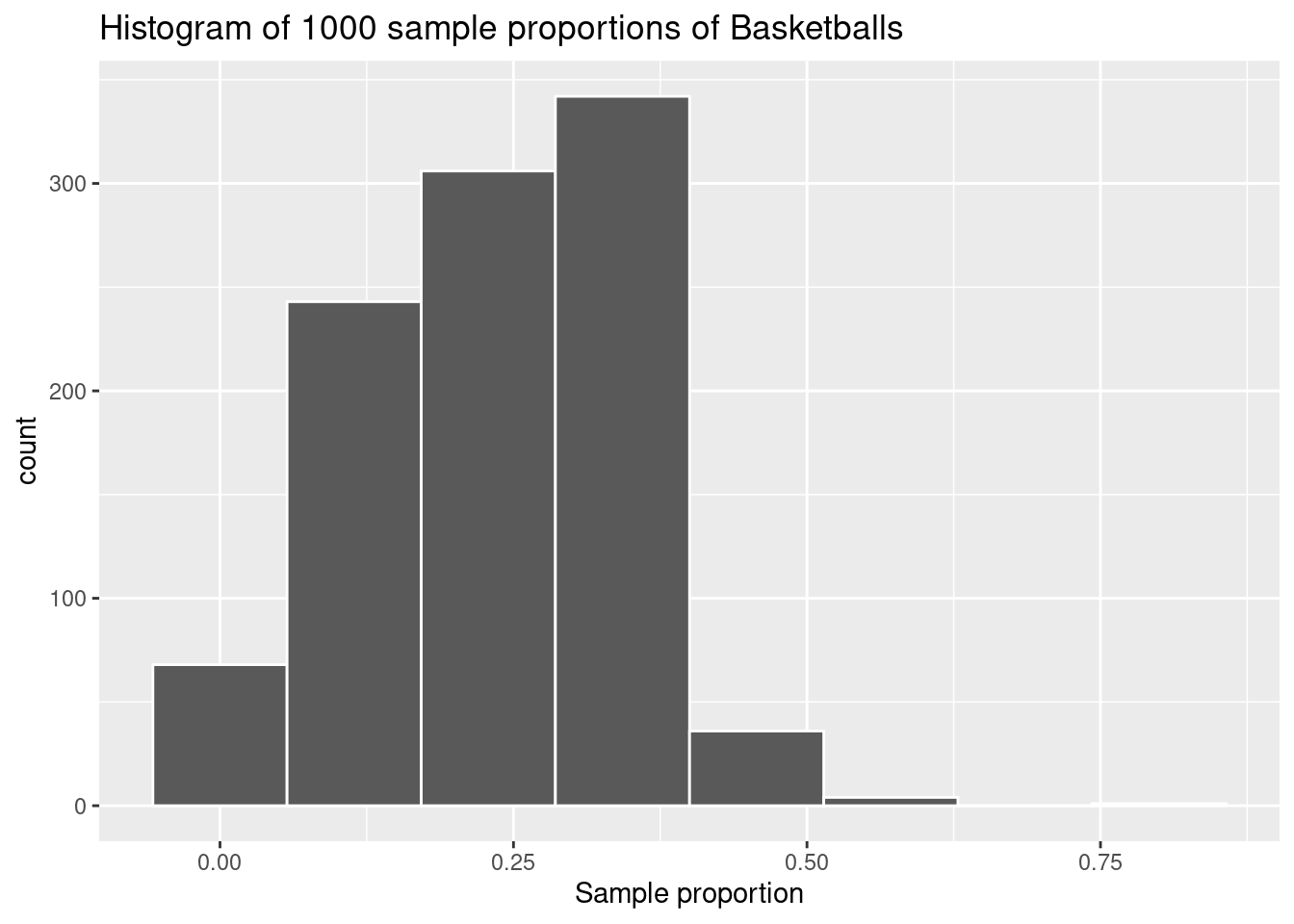
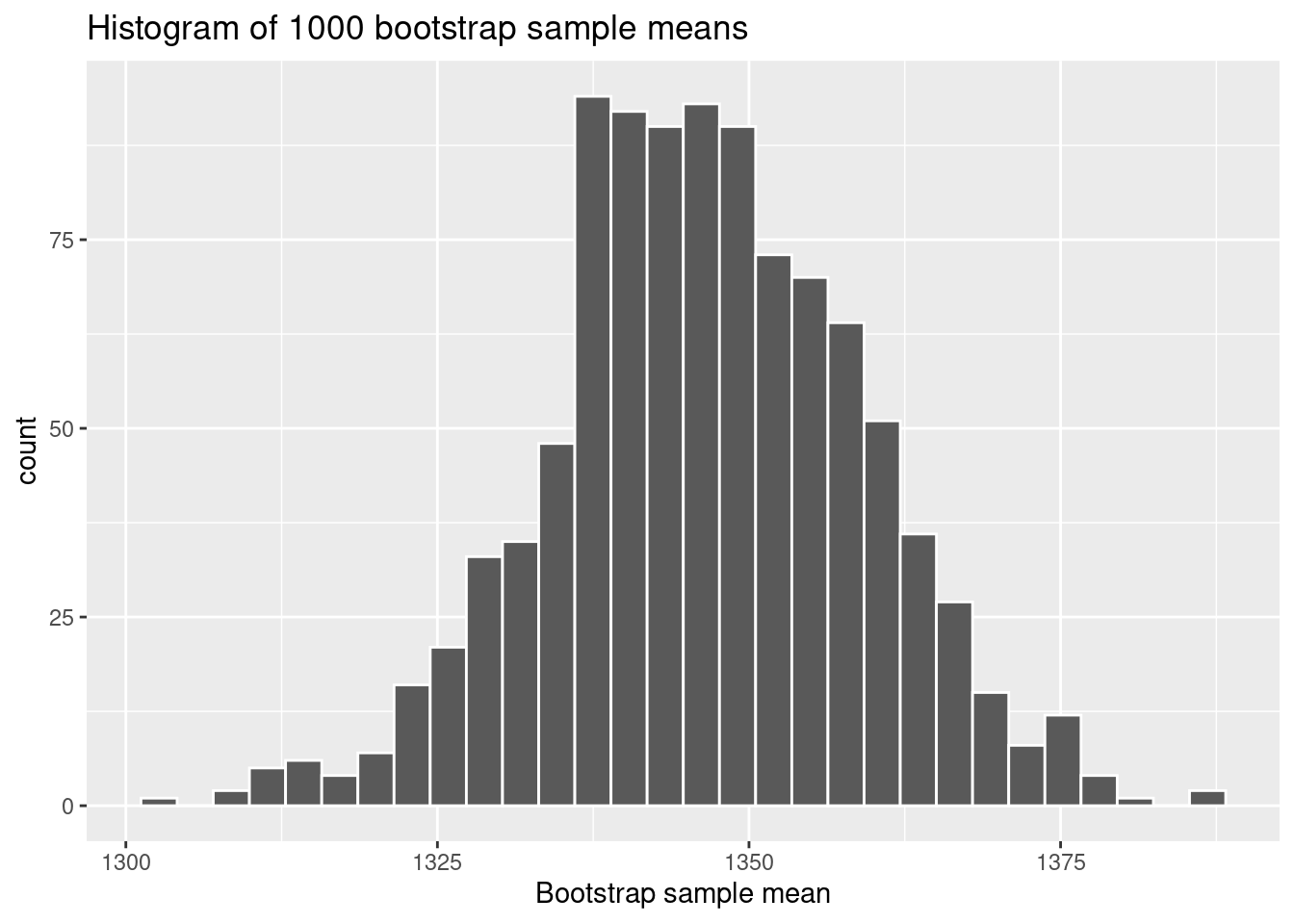
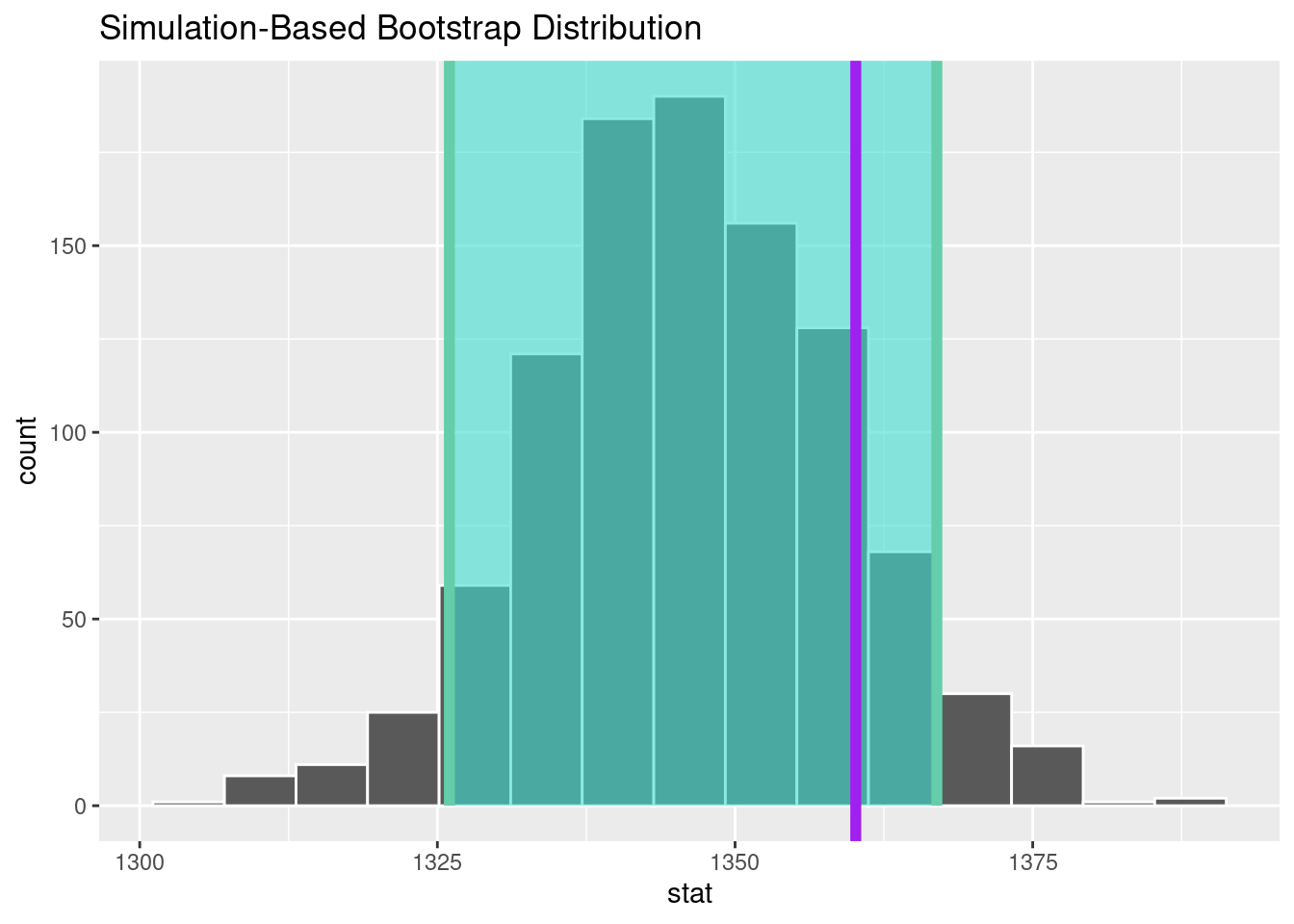
# Load the required packages
library(dplyr)
Attaching package: 'dplyr'The following objects are masked from 'package:stats':
filter, lagThe following objects are masked from 'package:base':
intersect, setdiff, setequal, unionlibrary(ggplot2)
library(moderndive)
library(infer)# For reproducibility
set.seed(2024)
# Create vectors of sport ball types and their proportions
types_of_sport_balls <- c("Basketball", "Pickleball", "Tennis Ball",
"Football/Soccer", "American Football")
proportion_of_each_type <- c(0.2, 0.15, 0.3, 0.25, 0.1)
# Create a tibble of 1200 sport balls that will act as our population
store_ball_inventory <- tibble(
ball_ID = 1:1200,
ball_type = sample(x = types_of_sport_balls,
size = 1200,
replace = TRUE,
prob = proportion_of_each_type
)
)# Use glimpse to explore the structure of the dataset
glimpse(store_ball_inventory)Rows: 1,200
Columns: 2
$ ball_ID <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 2…
$ ball_type <chr> "Pickleball", "Football/Soccer", "Basketball", "Basketball", "Football/Soccer", "Basketball", "Footb…# Create a count of ball_type
store_ball_inventory |>
count(ball_type)# A tibble: 5 × 2
ball_type n
<chr> <int>
1 American Football 117
2 Basketball 252
3 Football/Soccer 299
4 Pickleball 187
5 Tennis Ball 345# Determine the proportion of basketballs in the inventory
p_df <- store_ball_inventory |>
summarize(prop_bball = mean(ball_type == "Basketball"))
# Convert p to a numeric value
p <- p_df$prop_bball
# Or using the tidyverse
p <- p_df |> pull(prop_bball)
p[1] 0.21# Retrieve a sample of 10 balls from the inventory
ball_sample <- store_ball_inventory |>
slice_sample(n = 10, replace = FALSE)
# Determine the proportion of basketballs in the sample
ball_sample |>
summarize(prop_bball = mean(ball_type == "Basketball"))# A tibble: 1 × 1
prop_bball
<dbl>
1 0.4# Retrieve another sample of 50 balls from the inventory
ball_sample2 <- store_ball_inventory |>
slice_sample(n = 10, replace = FALSE)
# Determine the proportion of pickleballs in the sample
ball_sample2 |>
summarize(prop_bball = mean(ball_type == "Basketball"))# A tibble: 1 × 1
prop_bball
<dbl>
1 0.3# Use `rep_slice_sample()` from the `infer` package
ball_samples <- store_ball_inventory |>
rep_slice_sample(n = 10, reps = 1000, replace = FALSE)
ball_samples# A tibble: 10,000 × 3
# Groups: replicate [1,000]
replicate ball_ID ball_type
<int> <int> <chr>
1 1 940 Basketball
2 1 1052 American Football
3 1 749 Football/Soccer
4 1 497 Tennis Ball
5 1 1081 Tennis Ball
6 1 737 Basketball
7 1 979 Pickleball
8 1 944 Tennis Ball
9 1 1112 Tennis Ball
10 1 855 Tennis Ball
# ℹ 9,990 more rows# Determine sample proportions with `dplyr`
props_bball <- ball_samples |>
summarize(prop_bball = mean(ball_type == "Basketball"))
# Create a histogram of the sample proportions with 8 bins
ggplot(props_bball, aes(x = prop_bball)) +
geom_histogram(bins = 8, color = "white") +
labs(x = "Sample proportion",
title = "Histogram of 1000 sample proportions of Basketballs") 
# Using the simulations, calculate the standard deviation of the
# sample proportions
se_sample_props <- props_bball |>
summarize(sd(prop_bball)) |>
pull()
# Using the formula for the standard error of a sample proportion
n <- 10
se_sample_props_formula <- sqrt(p * (1 - p) / n)
se_sample_props_formula[1] 0.1288022# Here's the function from the walkthrough to calculate the standard error
se_sample_props <- function(size, repetitions = 1000, type = "Pickleball") {
props <- store_ball_inventory |>
rep_slice_sample(n = size, reps = repetitions, replace = FALSE) |>
summarize(prop = mean(ball_type == type))
se_sample_props <- props |>
summarize(sd(prop)) |>
pull()
return(se_sample_props)
}
# Use the function to calculate the standard error for a sample size of 10
# with 2000 repetitions for Basketball
se_sample_props(10, 2000, "Basketball")[1] 0.130401Assume we have information about the population of homes in Phoenix, AZ. We are interested in their use of electricity factoring in that some homes do not have air conditioning and only use fans.
# For reproducibility
set.seed(2024)
# Number of homes in each group
n_ac <- 0.8 * 600000
n_fans <- 0.2 * 600000
# Simulate electricity usage (in kWh) for homes with AC
ac_usage <- rnorm(n_ac, mean = 1500, sd = 300) # Higher mean for AC usage
# Simulate electricity usage (in kWh) for homes using fans
fan_usage <- rnorm(n_fans, mean = 800, sd = 150) # Lower mean for fan usage
# Combine into a single data frame
electricity_usage_phoenix <- tibble(
home_ID = 1:(n_ac + n_fans),
cooling_system = c(rep("AC", n_ac), rep("Fans", n_fans)),
usage_kWh = c(ac_usage, fan_usage)
)
# View the data
electricity_usage_phoenix# A tibble: 600,000 × 3
home_ID cooling_system usage_kWh
<int> <chr> <dbl>
1 1 AC 1795.
2 2 AC 1641.
3 3 AC 1468.
4 4 AC 1436.
5 5 AC 1847.
6 6 AC 1888.
7 7 AC 1660.
8 8 AC 1462.
9 9 AC 1133.
10 10 AC 1164.
# ℹ 599,990 more rows# Choose sample size
sample_size <- 1000
# Generate a sample
set.seed(2024)
usage_sample <- electricity_usage_phoenix |>
slice_sample(n = sample_size, replace = FALSE)
# Calculate the sample mean
sample_mean <- usage_sample |>
summarize(mean(usage_kWh)) |>
pull()
sample_mean[1] 1346.212# Calculate the standard deviation
sample_sd <- usage_sample |>
summarize(sd(usage_kWh)) |>
pull()
sample_sd[1] 399.186# Calculate the population mean
population_mean <- electricity_usage_phoenix |>
summarize(mean(usage_kWh)) |>
pull()
mu <- population_mean
mu[1] 1360.137# Calculate the population standard deviation
population_sd <- electricity_usage_phoenix |>
summarize(sd(usage_kWh)) |>
pull()
sigma <- population_sd
sigma[1] 393.7991# Calculate the margin of error for a 90% confidence interval
z_star <- qnorm(p = 0.95) # Assumes a normal distribution
margin_of_error <- z_star * (sigma / sqrt(sample_size))
# Recall the point estimate
point_estimate <- sample_mean
# Calculate the confidence interval
lower_bound <- point_estimate - margin_of_error
upper_bound <- point_estimate + margin_of_error
# Display the confidence interval
c(lower_bound, upper_bound)[1] 1325.729 1366.696# Remember the population parameter (we usually don't know it)
between(mu, lower_bound, upper_bound) # dplyr::between()[1] TRUE# Calculate the margin of error for a 90% confidence interval
t_star <- qt(p = 0.95, df = sample_size - 1) # t-distribution
margin_of_error_t <- t_star * (sample_sd / sqrt(sample_size))
# Same point estimate
point_estimate_t <- sample_mean
# Calculate the confidence interval
lower_bound_t <- point_estimate_t - margin_of_error_t
upper_bound_t <- point_estimate_t + margin_of_error_t
# Display the confidence interval
c(lower_bound_t, upper_bound_t)[1] 1325.429 1366.995# Remember the population parameter (we usually don't know it)
between(mu, lower_bound_t, upper_bound_t)[1] TRUEWe are “95% confident” that the true mean commute time for this population of Phoenix houses is between 1325.4294955 and 1366.9952348 kilowatt-hours. This is the same as saying that if we were to take many samples of size 100 and calculate the confidence interval for each sample, we would expect 95% of those intervals to contain the true population mean of 1360.1370117.
# Assume we only have a sample of 1000 homes and their electricity usage
usage_sample# A tibble: 1,000 × 3
home_ID cooling_system usage_kWh
<int> <chr> <dbl>
1 86565 AC 1826.
2 532090 Fans 625.
3 127999 AC 1738.
4 597164 Fans 503.
5 121242 AC 1183.
6 53451 AC 1397.
7 132457 AC 1132.
8 503380 Fans 1022.
9 256276 AC 1491.
10 418903 AC 1201.
# ℹ 990 more rowsinfer Frameworkinfer framework you have seen so far to calculate bootstrap statisticsStart with the data and then |> into the following functions:
- specify(): Define the variable of interest
- generate(): Create the bootstrap samples
- calculate(): Calculate the statistic of interest
- visualize(): Visualize the bootstrap distribution
# Bootstrapping the sample
set.seed(2024)
one_bootstrap <- usage_sample |>
specify(response = usage_kWh) |>
generate(reps = 1, type = "bootstrap")
one_bootstrapResponse: usage_kWh (numeric)
# A tibble: 1,000 × 2
# Groups: replicate [1]
replicate usage_kWh
<int> <dbl>
1 1 1933.
2 1 1733.
3 1 947.
4 1 1497.
5 1 1980.
6 1 1334.
7 1 784.
8 1 1175.
9 1 1593.
10 1 1431.
# ℹ 990 more rows# Calculate the mean of the bootstrap sample
one_bootstrap |>
calculate(stat = "mean") |>
pull()[1] 1332.641# Bootstrapping 1000 samples
many_bootstraps <- usage_sample |>
specify(response = usage_kWh) |>
generate(reps = 1000, type = "bootstrap")
many_bootstrapsResponse: usage_kWh (numeric)
# A tibble: 1,000,000 × 2
# Groups: replicate [1,000]
replicate usage_kWh
<int> <dbl>
1 1 727.
2 1 1757.
3 1 1343.
4 1 796.
5 1 1542.
6 1 1609.
7 1 2069.
8 1 1044.
9 1 2030.
10 1 1511.
# ℹ 999,990 more rows# Calculate the mean of each bootstrap sample
bootstrap_means <- many_bootstraps |>
calculate(stat = "mean")
bootstrap_meansResponse: usage_kWh (numeric)
# A tibble: 1,000 × 2
replicate stat
<int> <dbl>
1 1 1357.
2 2 1338.
3 3 1335.
4 4 1347.
5 5 1340.
6 6 1336.
7 7 1345.
8 8 1337.
9 9 1372.
10 10 1377.
# ℹ 990 more rows# Create a histogram of the bootstrap means
ggplot(bootstrap_means, aes(x = stat)) +
geom_histogram(bins = 30, color = "white") +
labs(x = "Bootstrap sample mean",
title = "Histogram of 1000 bootstrap sample means")
# Calculate the 90% bootstrap confidence interval in two ways since bell-shaped
bootstrap_percentile_ci <- bootstrap_means |>
get_confidence_interval(level = 0.90, type = "percentile")
bootstrap_se_ci <- bootstrap_means |>
get_confidence_interval(level = 0.90,
type = "se",
point_estimate = sample_mean)We are “95% confident” that the true mean electricity usage for this population of adults is between 1326.0090851 and 1366.9481513 kilowatt-hours. This is the same as saying that if we were to take many samples of size 100 and calculate the confidence interval for each sample, we would expect 95% of those intervals to contain the true population mean of 1360.1370117.
# Show the histogram of bootstrap means with the confidence interval
# and the population parameter (not usually known)
bootstrap_means |>
visualize() +
shade_confidence_interval(endpoints = bootstrap_percentile_ci) +
geom_vline(xintercept = mu, color = "purple", linewidth = 2)